The Black Scholes (Merton) model has revolutionized the role of options and other derivatives in the financial market. Its creators Fischer Black, (Myron Scholes) and Robert Merton have even won a Nobel Prize for it in 1997. Still today, the Black Scholes model plays a huge role in the world of derivatives and options trading.
In this article, I will breakdown the Black Scholes formula, its implications about how options are priced, and much more. Even though, you will rarely directly use the model to calculate options prices, understanding the Black Scholes formula will give you a better and more in-depth comprehension of options.
Note that the Black Scholes model is a mathematical model and therefore, this article will cover the mathematics behind options pricing. Nevertheless, I will try to break down everything as easy and intuitive as possible. This will, hopefully, give you a different perspective on options than what you usually learn.
I would not recommend this article to complete options trading beginners. You should at least have some knowledge about options basics. If you are new to options, check out my free options trading beginner course.
What is the Black Scholes Model?
The Black Scholes model is a mathematical model that models financial markets containing derivatives. The Black Scholes model contains the Black Scholes equation which can be used to derive the Black Scholes formula. The Black Scholes formula can be used to model options prices and it is this formula that will be the main focus of this article.
So without further ado, here is the Black Scholes Formula:

I know it looks intimidating. So don’t worry if you don’t understand anything yet. I will slowly breakdown every aspect of this formula throughout this article.
Assumptions behind the Black Scholes Model
Let us start with some of the most important assumptions behind the Black Scholes model:
- The options are European style options (only exercisable at expiration)
- Trading doesn’t cost anything (no commissions)
- There exists a constant risk-free rate at which one always can borrow/lend money
- Stock prices follow a log-normal distribution and volatility is constant
- Stocks do not pay dividends
- Markets are efficient (no possibility for arbitrage)
There are extensions to the Black Scholes model in which these assumptions are relaxed. These, however, are even more complicated and not covered in this article.
Even though some of these assumptions do not accurately reflect reality, the Black Scholes model is still one of the best and most commonly used options pricing models. But it certainly isn’t a perfect model. Nevertheless, it is still extremely relevant for all options traders.
The Black Scholes Formula Explained
Now, let’s actually start breaking down the different components of the Black Scholes formula. I will start by presenting the formula for the price of call options.
For this, let’s start by understanding the different variables:
- C(S, t) is the price of a call option at time t on a stock with price S.
- N( ) is the cumulative distribution function. This function just outputs a probabilistic value that is used in the formula.
- T is the time left until the expiration date, in years. T is expressed as the difference between T1 (expiration date) and t (the current date).
- S is the current price of the underlying stock.
- K is the strike price of this call option.
- r is the constant risk-free rate.
- σ is the (implied) volatility of the underlying stock.
With that out of the way, let’s start focusing on the actual formula itself:
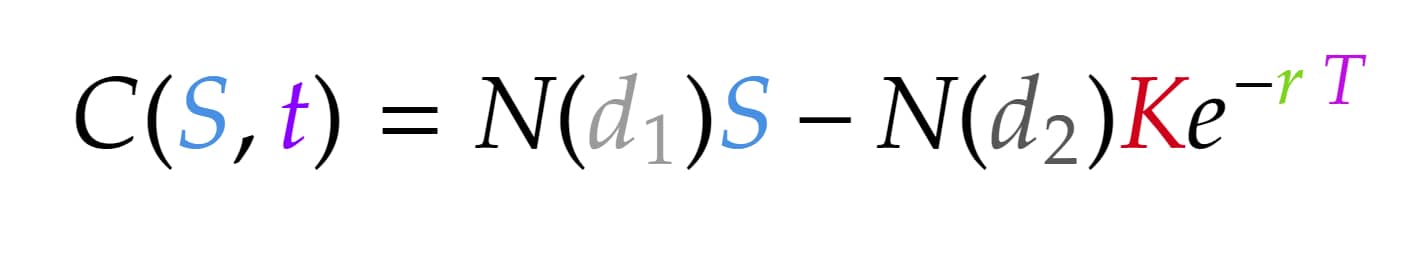
First off, I will present some simplified intuition behind the Black Scholes formula. If you were to calculate an option’s price yourself, you would probably start with an option’s intrinsic value. For call options, intrinsic value is the following:
Intrinsic value = Stock Price – Strike Price
In the Black Scholes formula notation, this would be:
Intrinsic value = S – K
This is exactly what you get when you plug in 0 for T which would be the option’s price at expiration in the Black Scholes formula. In other words, at expiration, an option will only have extrinsic value left.
This simplified formula should make intuitive sense as a call option with a strike price less than the underlying price should be worth at least as much as the difference. Otherwise, you could immediately exercise your call option for a riskless profit. Furthermore, a call option with a strike price above the underlying price is Out of The Money (OTM) and should be worth less than an In The Money (ITM) option.
However, if you only look at intrinsic value, all OTM options are worth nothing. This doesn’t seem right which is exactly the reason why there also exists extrinsic value.
Extrinsic value is the value of an option that is not determined by its difference between the underlying price and the strike price. Factors affecting the extrinsic value are time till expiration, the volatility of the underlying asset and a few more. For instance, the more time an option has left till its expiration date, the more time the underlying price has to move and thus it should be priced higher than an option with only a little time left until expiration.
The total price of an option can be expressed as follows:
Option Price = Intrinsic Value + Extrinsic Value
Or to put it differently:
Call Option Price = (S – K)⋅X = X⋅S – X⋅K
Where (S – K) is the intrinsic value and X is some way of expressing extrinsic value. I hope you can see the similarity between this formula and the Black Scholes formula.
What we just did was a very simplified version of deriving the Black Scholes formula. Hopefully, this gives you some intuition behind the formula.
A Closer Look at the Black Scholes Formula

Now let’s dig a little deeper. By now, you hopefully understand that all the Black Scholes formula is, is a more precise version of the above-derived formula. As you now know, it is very easy to find the intrinsic value of an option. But what exactly goes into an option’s extrinsic value?
To answer this question, let’s take a look at the multipliers of S (Stock Price) and K (Strike Price). K the strike price is multiplied by e-r T and by N(d2). The first multiplication K ⋅ e-r T basically just discounts the strike price to the current time. It does this by comparing the strike price to the risk-free rate and the time till expiration. The reason why this is done is that an option’s price should be affected by the risk-free rate.
For instance, if you could receive the same payoff with a completely riskless investment as with a risky option, you would never choose the option. Therefore, an option’s price reflects the potential return that you could receive from now until expiration at the risk-free rate.
Now, let’s look at N(d1) and N(d2), the other two remaining multipliers of S and K. N( ) is the cumulative distribution function which is used to calculate probabilities under a normal distribution (a bell-curved distribution curve). This means that N( ) just outputs a probability value between 0 and 100%.
In simplified terms, N(d2) calculates the estimated probability that the option will be exercised. This only makes sense, when the option is ITM or, in other words, when S (stock price) is greater than K (strike price). So you could also say, that N(d2) is a risk-adjusted estimate of the probability that the future stock price will be above the strike price at expiration.
Factors that go into this probability are:
- Time till expiration. The more time there is left, the higher the chances that the underlying price will move above the strike price.
- Volatility. More volatile stocks move much more and subsequently have better odds of breaching the strike price before expiration.
- (Stock price, strike price, risk-free rate)
Many broker platforms, including Tastyworks, show the probability of an option expiring ITM. This value is usually N(d2) or some slightly modified version of N(d2).
It is harder to directly interpret N(d1), however, you can try to think of it as the risk-adjusted probability that the option won’t be exercised. As visible from the formula for d1, N(d1) is always greater than N(d2), regardless of the variable values. This makes sense, as the value of an option should never be negative. N(d1) can also be thought of as the option Greek Delta of the call option (the option’s sensitivity to changes in the stock’s price), but more on that later.
I created the following image to sum up, some of the simplified explanations of each component of the Black Scholes formula:
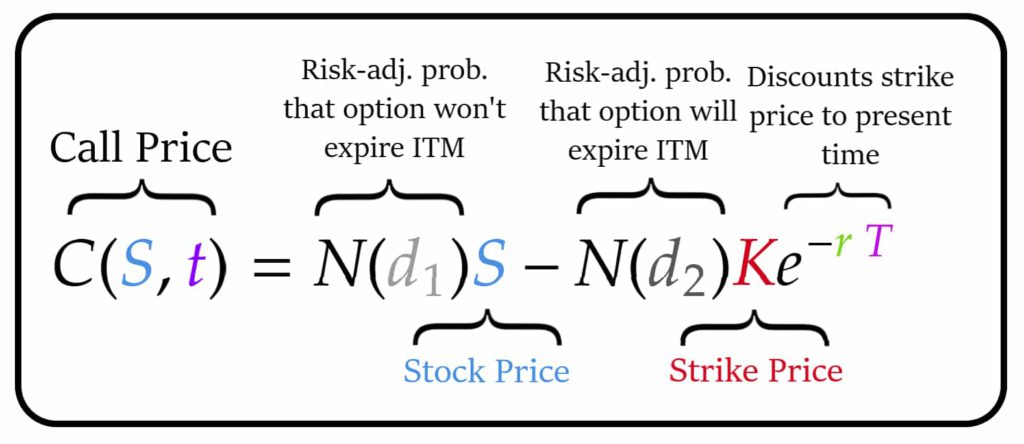
Note that this is just one simplified way of understanding and interpreting the Black Scholes formula. If you are looking for a very high-level mathematical explanation, this is not the right place.
If you want to see the Black Scholes formula in action, make sure to check out The Strategy Lab. It allows you to visually see and interact with the Black Scholes formula.
(Implied) Volatility and the Black Scholes Formula in Practice
Now let us talk about the role of volatility in the Black Scholes formula. First of all, why should volatility even affect an option’s price?
Imagine two stocks, XYZ and ABC that are both at $100 and are identical in every aspect except for their volatility. XYZ is about twice as volatile as ABC. Now, you have to choose between buying a call option with a strike price of $110 on XYZ or ABC (same price). The logical choice would be the XYZ option because XYZ is more volatile and thus, more likely to move up and beyond $110 than ABC.
In conclusion, more volatile stocks should have higher-priced options because they offer more profit opportunities.
With that being said, it shouldn’t only be past volatility that determines the volatility value of an option. Instead, it should be the volatility between now and the option’s expiration date. Therefore, the Black Scholes formula uses the annualized standard deviation of the return on the stock as a measure of volatility (σ). This is also referred to as implied volatility.
The only problem is that implied volatility is the only input of the Black Scholes formula that isn’t directly observable. It isn’t observable because we don’t know the distribution of the future returns of a stock.
But if we don’t know one of the inputs of the Black Scholes formula, how can we use it to calculate an option’s price?
The answer to this question is, we don’t. In practice, the Black Scholes formula is commonly not used to calculate an option’s price. Options’ prices usually are already known and directly observable in the market. Instead, the Black Scholes formula is commonly used to calculate the implied volatility of options.
By transforming the Black Scholes formula and then inputting all the observable values (including the option’s price), we can derive an option’s implied volatility. The derived implied volatility can, for instance, be used to make estimates of the future volatility of an asset.
Otherwise, the Black Scholes model is often used to calculate theoretical option’s prices by inputting theoretical implied volatility. This can be useful to simulate and analyze potential options trades.
Put-Call Parity
So far, we have only talked about calculating the price of a call option. However, the Black Scholes formula can also be used to calculate the price of a put option. To do this, we could use a similar formula as the one for the call option (with the same parameters):
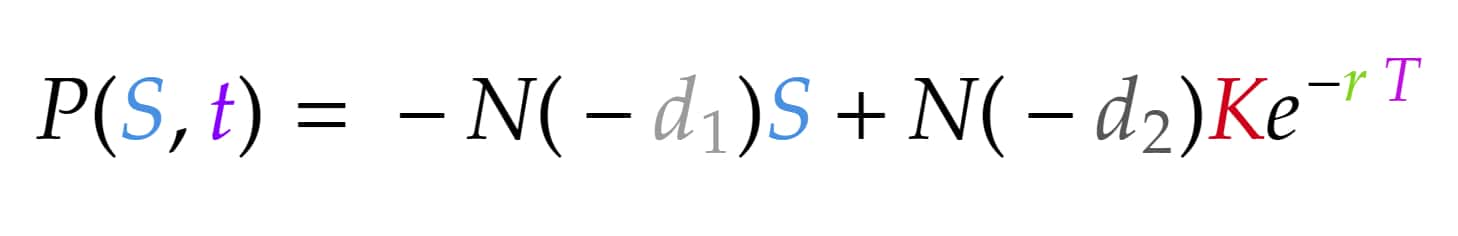
There is, however, an easier alternative to finding the price of a put option. As we already did all the work to derive the price of a call option, we can just use the relationship between call and put option prices to arrive at a put option price.
The relationship between a call and a put option with the same strike price, underlying asset and expiration date is the following:
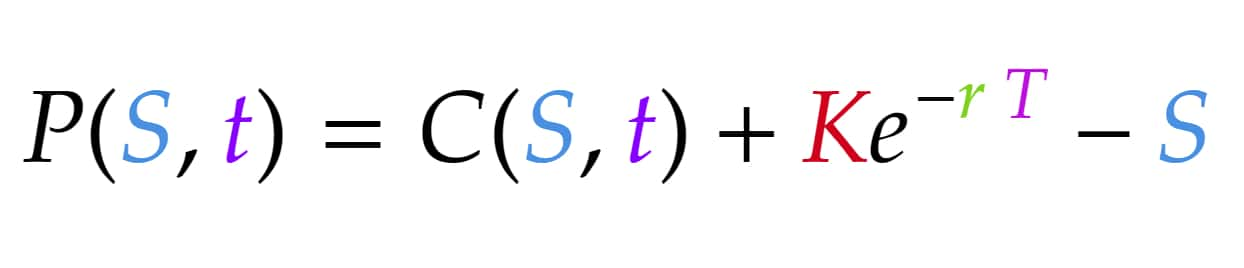
P(S, t) is the price of the put option at time t on stock S. The other factors are the same as before.
This formula is based on the thought that a simultaneous position of a long call and (equivalent) short put option behaves the same as a forward contract at the strike price and the same expiration date as the options. This is also known as put-call parity.
The Greeks
Next up, let’s take a look at what the Greeks have to do with the Black Scholes formula. As you might or might not know, Greeks measure changes in an option’s price for changes in certain market factors. In other words, they measure an option’s price sensitivity to changes in certain market factors.
Mathematically speaking, they are partial derivatives of the different parameters of the Black Scholes formula. I will not cover the mathematical formula for each Greek in this article. Instead, I will briefly explain what each Greek measures:
- Delta measures the option’s price sensitivity to changes in the underlying’s price. A Delta of 0.3 means that the option’s price would increase by $0.3 for a $1 increase in the underlying’s price. Delta for call options is N(d1) and N(d1) – 1 for put options.
- Gamma measures the rate of change of Delta. So it is the partial derivative of Delta. Gamma is calculated the same way for call and put options.
- Theta measures an option’s sensitivity to changes in time till expiration (time decay). This means Theta shows you how much value an option gains or loses for the passing of time.
- Vega measures an option’s sensitivity to changes in implied volatility. Just like for Gamma, the formula for Vega is the same for call and put options.
- Rho measures an option’s sensitivity to changes in the risk-free rate.
Even though the Greeks are calculated through the partial derivatives of the different parameters of the Black Scholes formula, they are usually also adjusted. For instance, Theta is adjusted so that its value represents the option’s price sensitivity for the change of one day instead of one year in the time till expiration.
Greeks are very commonly used in the world of (options) trading as they are a great tool to measure your risk toward certain market factors. This gives you a great basis to manage your positions and exposure.
In practice, the Greeks aren’t only used for single option positions. Instead, they are commonly used to measure different risks of an entire portfolio. This can be done by summing up the values of the same Greek for every position.
Some Flaws of the Black Scholes Model
Last but not least, let’s talk about some of the imperfections of the Black Scholes model. The easiest way to criticize the Black Scholes model is to look at its assumptions. Here are some of the assumptions that certainly don’t reflect real-world conditions:
- Costless trading: In reality, trading costs money in the form of commissions, slippage, clearing fees, liquidity problems and more. This is especially true in the world of (often thinly-traded) options.
- Efficient markets: The Black Scholes model assumes that the markets are 100% efficient and allow for no arbitrage opportunities. This is provably incorrect.
- European options: The Black Scholes model models European options, even though American options (that can always be exercised) are far more common.
- No dividends: The original Black Scholes model allows for no dividends, which isn’t the case in reality.
- Risk-free rate: There is no such thing as a risk-free rate. Even though assets such as certain government bonds have very low risk, they aren’t completely riskless.
- Continuous trading: The Black Scholes model assumes that trading never halts. In reality, most trading pauses every night and at the weekends.
- Distribution of returns: The Black Scholes model assumes a normal distribution of returns. This is often not the case in reality. Furthermore, a normal distribution downplays the likelihood of big moves a lot! Statistically, big moves are far more likely than according to the model.
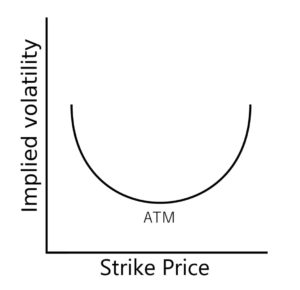
Another popular criticism of the Black Scholes model is the Volatility Smile:
According to the Black Scholes model, the implied volatility of different options on the same underlying should be the same. However, if you compare the computed volatilities of options (on the same underlying) with different strikes, this is not the case. Instead, the implied volatility tracked against the different strike prices often forms a curve that looks like a smile.
With that being said, the Black Scholes model is still one of the most commonly used options pricing models. It is very easy to use, quite robust and generally, still very useful. Furthermore, there exist countless extensions of the model that relax some of the above-mentioned assumptions. Therefore, the Black Scholes model is still an excellent model of derivatives in financial markets.
Conclusion
I really hope this breakdown of the Black Scholes model could further develop your understanding of the options market by showing you the mathematical model on which most of it is based.
I hope this article helped you understand how exactly options are priced and where things such as the Greek, the probability of ITM and other key options trading factors actually come from.
Even though the Black Scholes model isn’t perfect, it and extensions of it are still the most common way of modeling options and other derivatives in the financial markets.
If you want to see the Black Scholes formula in action and actually play around with it, I recommend checking out The Strategy Lab. The Strategy Lab was developed to give you a much better understanding of options pricing behavior through interactive visualization of the Black Scholes formula. It allows you to understand the Black Scholes formula without all the math:
Learn More About The Strategy Lab
If you have any questions or comments, please let me know in the comment section below.

wow, This is some interesting math. I actually purchase stock from time to time but I have never really learnt much about the math behind options. I do feel that this kind of math is a little bit over my level, it is however really interesting to learn about the black Scholes model and also how to use it. I do feel like the information you are providing is really valuable but I would need to take it in little by little as it is fairly complicated for me. Is there a specific way to think so that one would be able to learn this math or does practice make perfect?
Hi,
I just recommend going through the math step by step and trying to really understand every step before you move on, even if it takes some time. Thereby, you can slowly start combining the steps and understand the bigger picture.
Thank you Louis, once again worth every minute I spend reading and digesting it.
Awesome to see that you liked it!
Wow! This black Scholes is rather more difficult than what I anticipated. I never thought it would be this much cumbersome to analyse or understand. Well! I feel there is need for me to bookmark this post so that I can refer to it later on and to also be able to grasp the information fully. I’m an options trader but then, I have never tried this out. So, I feel a need to learn from the basice
Oh boy, this is going to take a minute to digest. So yeah that is quite a bit of math involved in deciphering the Black Scholes Model for options trading! I want to learn it but I’m definitely what you would call a beginner options trader. I see there is the lab to work on it, is that the best route for a total beginner like me? Thanks for any tips on the best way to learn this Black Scholes Model.
Hi,
Thanks for your comment. If you are completely new to options, I recommend first learning the options basics. This will give you a much better basis for understanding the Black Scholes model. You can learn all the basics in my free options trading beginner course.
But after that, The Strategy Lab will help you gain a much better understanding of the Black Scholes model and options pricing in general. The Strategy Lab shows you the Black Scholes formula in practice without all the math. This makes it much more beginner friendly.
As someone that is fairly well versed with options this was a little confusing to me. I am one that learns more with visual explanations that just equations. Not to say that I dont do well with Math was always in the top 5 in my math classes. So mayne more visual explanations or even a video embedded to help others visualize the equation more easily. When you broke it day with the visual equation explaining chance to be exercised and chance to be ITM it made more sense. Very in depth coverage. Thank you
Thank you for the feedback. Usually, I try to avoid explaining options through math, but as the topic of this article is the Black Scholes formula and the math behind options I couldn’t really avoid the math. Really understanding all the math behind the Black Scholes model is quite hard. My goal was just to give some intuition behind the formula.
If you prefer some visualization of the Black Scholes formula, I recommend checking out The Strategy Lab.
I would like to compute the elements of option price individually. Intrinsic value is easy, but implied volatility (IV) and time value are more difficult.
I think that given a particular option price the BS equation can be solved numerically for IV but the answer is a percentage. I need a dollar value to make it the same units as time value. Also, what procedure do you recommend for calculating static time value (not time value decay)?
Hi Sam,
Thanks for your comment. I am not sure if I entirely understand your question. So definitely correct me if my answer doesn’t fit.
First of all, IV is a theoretical measure of an option’s relative value. It allows you to compare option’s prices across different underlying’s since it accounts for the other factors (underlying’s price, time…). So you can think of IV not as a factor that affects the option’s price, but as the option’s price itself expressed in a different unit.
You can certainly solve the BS equation for IV, but this won’t result in a measure of the IV part of the option’s price. It will simply give you the theoretical IV value.
Furthermore, the terms ‘time value’ and ‘extrinsic value’ of an option are often used interchangeably since it is time that dominates extrinsic value. If, for instance, there is no time left till expiration, there also is no extrinsic value left. In that sense, it doesn’t really make sense to try to isolate time and IV value since they are so heavily interlinked.
I hope this helps. Definitely let me know if I misunderstood your question.