This article is the first lesson of the Intermediate Options Trading course. It is all about how options are priced and what affects their prices (aka. The Greeks). This is one of the essential lessons for every options trader. It is extremely important to understand options pricing. Therefore, please take your time when going through this lesson and ask questions in the comment section if you have trouble understanding some of the contents. Don’t worry if you don’t understand everything the first time. You can always retake the lesson. Just don’t do the mistake of skipping ahead without understanding everything presented in this lesson. I have tried to explain everything as simple as possible. I have implemented an explanatory video, images, examples, an infographic and more to make the learning experience as ideal as possible.
The contents covered in this lesson aren’t complete basics anymore. To understand everything, you should already have a fundamental understanding of options. If you don’t have this, I recommend taking my Free Options Trading Beginner Course.
Video Lesson:
The Video Lesson below covers almost all the same concepts as the article below. If you prefer watching videos over reading, you should check out the video. But I really recommend watching the video and reading the article for the best learning effect.
How are Options Priced

There is a simple formula for option’s prices: Extrinsic Value + Intrinsic Value = Option’s Price
Intrinsic Value is the amount that an option is in the money (ITM). So the difference between the underlying’s price and the strike price of an ITM option. (Call options are ITM if their strike price is below the underlying’s price and put options are ITM if their strike price is greater than the underlying asset’s price.)
I will try to illustrate this with an example. Let’s say XYZ is trading at $150. If you would buy a call option at the 140 strike price, the call option would have an intrinsic value of $10 ($150 – $140 = $10). However, a call option with a strike price of 155 would have no intrinsic value at all because it isn’t ITM.
A put option at the 140 strike price (still on XYZ) would also have no intrinsic value. The 160 strike put option would have an intrinsic value of $10 ($160 – $150 = $10).
The deeper an option is in the money (ITM), the greater the intrinsic value becomes. Therefore, deep ITM options are more expensive than at the money (ATM) or out of the money (OTM) options. All OTM options have no intrinsic value.
Extrinsic Value is the remaining value of an option. There are multiple factors that affect the extrinsic value of an option. These factors are time left until expiration, the expected volatility (IV) and some less important factors like interest rates. When buying options, more time left until expiration will be an advantage as the underlying asset will have more time to move in the correct direction.
It makes more sense to buy an option with 100 days left until expiration than with 10 days left until expiration if the option requires the underlying asset to move $10 to become profitable. It is just much more likely that the underlying will move this far in 100 days than in 10 days. Therefore, options with more time left until expiration are more expensive. The more time left until expiry, the more expensive options become. The option with 100 days left until expiration can easily be 10x more expensive than the option with 10 days left until expiration. Therefore, choosing an option with more time left isn’t always the best choice.
Another major factor of extrinsic value is implied volatility. The higher the expected volatility becomes, the more expensive options become. This is because an increased volatility creates more opportunities. If an asset is expected to move much more than usual, you can potentially profit more as the asset will potentially move more than it usually does. Options allow you to profit from bigger moves and therefore they become more expensive.
Furthermore, there are other minor factors like interest rates or dividends that affect an option’s value. But these aren’t as relevant as the other factors. A factor like interest rates mainly becomes relevant for very long-term options (aka. LEAPS).
An option’s price can be estimated through advanced formulas like the Black-Scholes model. But this is a topic for a different, more-advanced lesson.

Summed up an option’s price consists of two parts:
1. Intrinsic Value:
- Intrinsic Value is the amount that an option is ITM
2. Extrinsic Value:
- Time Left Until Expiration
- Implied Volatility
- Other Minor Factors
If intrinsic value wouldn’t exist, option traders could easily make risk-free profits. To make this clear, I will give you a brief example:
Let’s say stock ABC is trading at $50. An option trader chooses to buy a call option with the $40 strike. The option’s extrinsic value is $3. The intrinsic value would be $10 ($50 – $40). Therefore, the option would cost him $13 (*100 = $1300 as a standard option contract controls 100 shares of stock). But if the intrinsic value wouldn’t exist, he would only have to pay $3 (*100 = $300). A call option gives its owner the right to buy the underlying asset at the strike price. Therefore, the buyer of this call option could immediately exercise his option and buy 100 shares of ABC for $40 per share. He could then proceed by selling these shares at $50 per share.
This would leave him with a profit of $700 (-$300 for the option – $4000 when buying the 100 shares for $40 per share + $5000 when selling the 100 shares for $50 per share). These trades could be executed within seconds.
If the option buyer would do the exact same but with paying for the intrinsic value of the option, he would end up with a $300 loss (-$1300 for the option -$4000 when buying the 100 shares for $40 per share + $5000 when selling the 100 shares for $50 per share).
As you can see, intrinsic value prevents arbitrage trades.
Option Greeks Explained
You might have stumbled upon option Greeks before. The Greeks are an essential part of options trading. A common analogy is that option Greeks are as important to trading options as a steering wheel and dashboard is to driving a car. Greeks basically give you an overview of what is going on in your position(s). Some Greeks are more important than others. Nevertheless, you should be aware of almost all of them all the time.
Somehow a common misconception is that Greeks are this overly complicated thing. I will try to break down the Greeks as simple as possible so that you can understand their importance and implement them into your own trading. But keep in mind that I will only cover the basics of these Greeks here.
What are Option Greeks
Option Greeks measure price changes in the option’s price for changes in the relevant factors. One greek for example measures price changes in the option’s price for price changes in the underlying asset. Other factors are time left until expiration, implied volatility… (so basically all the factors that impact an option’s price).
Delta
Let’s start with Delta. Delta is a relatively simple but still very important Greek. Delta measures the amount that the option’s price is expected to change for a $1 up-move in the underlying asset. I will try to simplify this with a brief example:
Stock ABC is trading at $200. You bought a call option that currently has a Delta of 40. This would mean that your position (1 long call) would gain $40 for a $1 up-move in ABC. If ABC would move up to $201, your position would gain $40. The same goes for the downside though. If ABC’s price would decrease to $199, the position would lose $40.
Delta is a great indicator of what you want the underlying asset to do. A bullish position usually has a positive Delta and a bearish position normally has a negative Delta. The greater Delta is, the more bullish the position becomes and the more negative Delta is, the more bearish your position becomes. A Delta-value near 0 means that your position is neutral.
Depending on your directional assumption, Delta can give you reasons to adjust your positions. For example, if you expect an asset’s price to go down but you have a position with positive Delta, you may want to adjust the position to fit your directional assumption.
Note that Delta and all the other Greeks aren’t constant. All Greeks change together with their factors.
Gamma
Gamma measures the rate of change of Delta for a $1 up-move in the underlying asset. Like I just said, Delta isn’t constant. Together with the underlying’s price Delta also changes. Once again, I’ll present this with a short example:
ABC is still trading at $200 and you still have an open long call position. In the previous example, the Delta of this call was 40 meaning that the position changes by $40 for a $1 change in ABC. Let’s say the Gamma for this position is 2. A Gamma of 2 would mean that Delta increases by 2 for a $1 up-move in ABC. The position would still gain $40 if ABC would move up to $201. But now Delta increases by 2 and therefore, Delta now is 42. Another $1 up-move in ABC would lead to a further $42 gain. The overall gain would then be $82.
If ABC’s price decreases by $1, Delta decreases by 2 as Gamma is 2. If ABC drops down to $198, the overall loss would be $78 ($40 + $38). So the loss for every $1 down-move decreases but the gain for every $1 up-move increases for long calls.
As you can see, Gamma can work in your favor or against you. Your losses can increase or decrease for every $1 move in the unwanted direction. The same can be the case for the gains as your gains also can become smaller or greater for each $1 move in the wanted direction.
But note that Gamma isn’t constant either. It also changes together with Delta and the price of the underlying asset.
Vega
The next important Greek is Vega. Vega measures the change in the option’s price for a 1% increase in implied volatility (IV). As we learned in an earlier lesson, implied volatility can change. Implied volatility usually increases when prices drop and it normally decreases as prices increase. In times of high implied volatility, options tend to be priced higher than in times of low IV. Therefore, option buyers can profit from a rise in IV, whereas option sellers profit from a decrease in IV. In times of high volatility, option sellers try to profit from decreasing IV.
This is also why Vega is negative for short option positions. A Vega of -20 means that a position would lose $20 for a 1% increase in IV. However, a Vega of -20 also means that a position would gain $20 for a 1% decrease in IV.
Long option positions have positive Vega-values as they profit from rising IV.
Vega and implied volatility should always be considered when trading options. As I just said IV tends to decrease for up-moves in the underlying asset’s price. Therefore, a bearish option position can still gain value even if the underlying asset increases in price if the position has a (very) negative Vega-value. In this case, the decrease in IV would offset the loss from the underlying asset’s move.
As you can see implied volatility can greatly impact your trading and it is very important to know if IV is high or low. Therefore, measures like IV Rank are essential for options traders. IV Rank can give you a very good idea of where IV currently is.
Vega isn’t constant either.
Theta
Yet another very important Greek is Theta. Theta is also known as time decay as it measures changes in the option’s price for the passing of 1 day. One main difference between stocks and options is that options expire after a certain time. This can greatly impact an option’s price. Options lose some of their value every day. This is the case because less time means less time for the underlying asset to move in your direction. In other words, less time leads to a decrease in the probability of profit (POP).
Theta or time decay can either be your biggest friend or your biggest enemy. If you are an option seller, Theta is your friend because you want the sold option to lose value so that you can buy it back for less than you initially received for it. If you are an option buyer, however, time decay works against you as your option(s) will lose some of their value every day.
A Theta of 10 would mean that the position gains $1o for the passing of one day if all other factors stay the same. A Theta of -5 would mean that the position loses $5 for the passing of one day if all other factors remain the same.
Theta isn’t constant either. It actually increases the closer an option gets to its expiration date. So an option with 10 days left until expiration loses much more of its value every day than an option with 100 days left until expiration.
Rho
Rho measures the change in the option’s price for a 1% change in interest rates. But as interest rates usually don’t change significantly overnight, this Greek isn’t as important as the other Greeks are. As long as you aren’t planning on trading very long-term options (aka. LEAPS), you can disregard this Greek.
The Greeks For Option Strategies
The Greeks of different options influence each other. When you combine different options to create a certain option strategy, the Greeks are added to each other. For example, a strategy with both a short call and a long call (at a higher strike price) will have more neutral Greeks than a single long call. Let’s simplify that with an example:
Stock XYZ is trading at $130. You buy 1 call option at the 140 strike price and sell 1 call option at the 135 strike price. The short call option has a Delta of -40 and the long call option has a Delta of 30. Therefore, the overall strategy has a Delta of -10. In other words, it is a slightly bearish strategy.
Furthermore, the sold call has a Theta of 20 meaning that it will gain $20 for the passing of one day (if everything else stays the same). However, the long call has a Theta of -15, so it loses $15 until the next day. This means that the overall strategy only has a Theta of 5 which means that the strategy will gain $5 every day. As Theta increases the closer the options are to their expiration date, this value will also increase slightly every day (if the remaining factors don’t change significantly).
I hope you get the point. Greeks of different options/positions influence each other. This is the case for all Greeks.
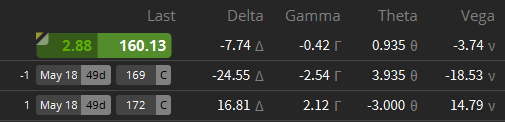
The Image above is a screenshot from my broker platform, Tastyworks. The screenshot shows an open credit spread (1 short call + 1 long call at a higher strike price). As you can see, all the Greeks (except for Rho) are displayed directly next to the Last price. The underlying asset was last traded for $160.13. The strikes of the options are 169 (for the short call) and 172 (for the long call). There are 49 days left until expiration. In the first line, the Greeks for the entire credit spread are displayed. The second row displays the Greeks for the short call only and the last line shows the Greeks for the long call only.
As you can see, the Delta-value of the long call is 16.81. From this, you might think this strategy is a bullish strategy. But as soon as you see the Delta-value of the short call, you should realize that the strategy actually is slightly bearish. It would profit from the underlying asset moving down. To be exact, the credit spread would earn about $7.5 for every $1 down-move in the underlying asset.
The credit spread also profits from time passing by and from a decrease in implied volatility. A 1% drop in IV would create a $3.74 gain in this spread (if everything else stays the same). The credit spread also earns almost $1 for the passage of one day (if the other factors remain the same). The short call even gains almost $4 every day. But this gain isn’t seen in the credit spread because the long call loses ca. $3 every day. (As there still is quite some time left until expiration, Theta is relatively low. Theta will increase the closer this spread will get to expiration.)
Side Note
The standard lot size for an option is 100. This means even though options often are quoted as if they were sold in singles, they aren’t. Usually, 1 option contract controls 100 shares of stock. Therefore, you often have to multiply the quoted option’s price by 100. If an option quote is $1.50, you have to multiply it by 100 to get the actual price of one option contract ($1.50*100 = $150).
The same goes for the Greeks. For some brokers, you will have to multiply the Greeks by 100. For example, some brokers tell you that the Delta for your position is 0.4 instead of 40. A Delta of 0.4 would mean that the option’s price increases by $0.4 for a $1 increase in the underlying asset. So if the option initially was worth $5, it would be worth $5.4 after a $1 increase in the underlying asset. Nevertheless, you still would have to pay $540 to purchase that option as the standard lot size is 100 and not 1 ($5.4*100 = $540).
Make sure to find out how your broker platform quotes the Greeks as there is a big difference between these two methods.
My broker platform, Tastyworks shows the Greeks like I explained them originally.
Recap
Option prices are affected by a variety of different factors. The Greeks measure price changes in the option’s price for changes in these different factors. It is very important to be aware of the Greeks when trading options (except for Rho). Greeks can give you a very good idea of how your position is doing and if/how you should adjust your positions.
To recap the basics of how options are priced, I created the following infographic. Hopefully, it helps with the understanding of the discussed concepts:

(If you want to use this infographic, go ahead. Just make sure to link back to this article.)
Free Cheat Sheet
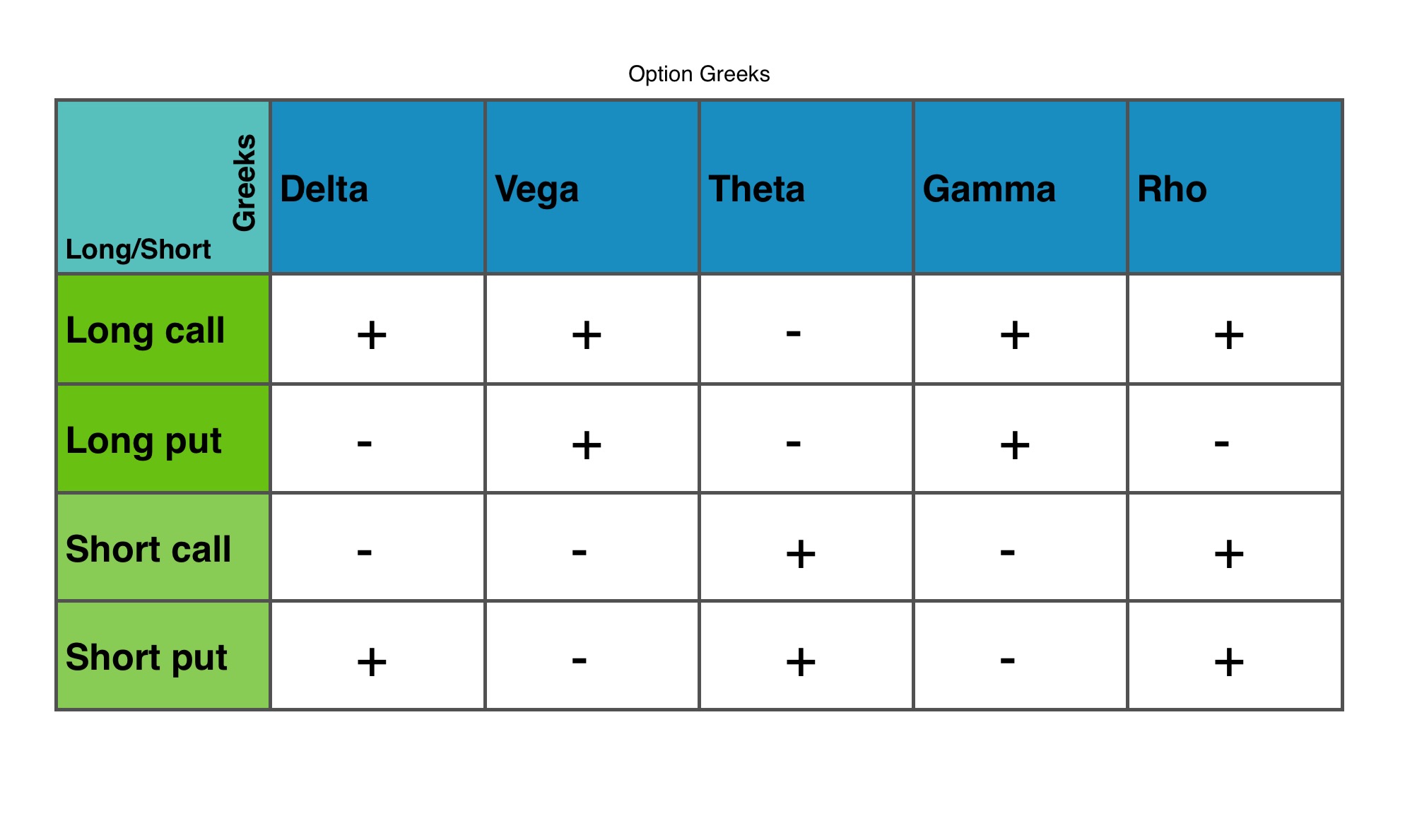
To see how certain option positions are affected by the different Greeks, I have created a table at the bottom of the page. It shows the impact of the Greeks on different positions.
A plus means that an increase in this factor will work in your favor, whereby a minus means that this factor is unfavorable to your position.
For example, Delta is positive for long calls meaning that the position will gain value for an increase in the underlying’s price. In other words, a long call is a bullish strategy.
A positive Vega means that the position will gain value from an increase in implied volatility. A negative Vega indicates that the position will gain value from a decrease and lose value for an increase in implied volatility.
A short put has a positive Theta meaning that time decay works in favor of this position…
I hope you understand how this table works and how it can help you understand the Greeks. The Greeks are something you will come across a lot in the future
So if you are interested in downloading or printing this helpful table, click here or the picture below.
I know this was a long and complicated lesson. But hopefully, you now have a good understanding of option prices and option Greeks. This knowledge is very important for option traders! If you have any questions, comments, feedback or anything else, PLEASE let me know in the comment section below!
This Article is part of the Intermediate Option Trading Course. If you are reading the article as a part of the course, you can continue to the next lesson: HERE

I love this chart at the end and you’re very clear explanations on The Greeks! I’ve been doing some research on options trading, but I have to admit that these “Greek terminologies” are a little intimidating at first.
That, and also most other people who explain them talk like an academic that is really hard to understand. I never really got Vega until I read this explanation on it. So thank you for that!
Also, I had never heard of Rho before, but it seems like it’s not something I really have to be concerned with at the moment since I am not current’y planning on getting into LEAPS.
It looks like you have a deep understanding on options. How long have you been trading them?
Hey Nick, I am so so glad to hear that you are enjoying and learning from my content! To learn more about me and my journey, check out the about me page.
Hi Louis,
Just visited your site dedicated to options trading and I liked it very much.You have very clearly explained how options are priced and option greeks. The chart that you have shown on your site is very helpful to understand more about option trading.I had a lot of doubts about option trading in my mind but I think with this much of study I will be able to make a good amount of profit from option trading.
Wow, very nice site you have there. I haven’t ever traded options but honestly your site looks very well done and informative, and I saw you have a beginner course. Its hard for me to offer any true advice because you definitely seem well educated on options and your site is really well organized.
you have taken an incredibly complicated topic and simplified this the best you can. the use of videos and content to help teach is a great idea. I feel I will rewatch and redo your training a few times as you suggest to ensure it really sinks in. For the first round, I do feel I have a really good understanding. I know I’ll have questions when I come back for the second round after letting this marinate!
So glad to hear that you enjoyed the lesson.
Hi,
Does the Tastyworks platform have a paper trade or virtual account to practice On?
Thanks
Great Question!
Sadly, Tastyworks does not have a paper trading feature yet. But they have already announced that they will add paper trading in the near future (2018).
You can check out all of Tastyworks features in my Tastyworks Review.
Wow! This article is very informative. I have been thinking about trying out my luck with trading for a while. But I just haven’t had the time to sit down and learn. With lesson I think that I would learn a lot. I like that for beginners you recommended your lesson for beginners. Thanks for all the information.
You are welcome. It’s a very good idea to sit down and educate yourself before risking any money.
This is in my “To Do” list as I am hearing a lot about this in the past. Online investing interests me much and options trading got me curious too. Your explanation here has helped me learn and understand how it works, although I’d admit it got me a little bit overwhelmed. I will try bookmark your post and return to it probably 2 or 3 more times, and then I will try it in actual. Thank you so much.
By the way, is there a way I can chat with you online?
Thanks for the comment. You can contact me HERE. It is a great idea to re-read the content until you fully understand it!
Excellent video and very good article!
Please check the following sentence – “A put option at the 140 strike price (still on XYZ) would also have no intrinsic value. The 160 strike put option would have an intrinsic value of $15 ($165 – $150 = $15).”
I think it should be:- *** …..intrinsic value of $10 ($160-$150=$10) ***
Let me know if I am wrong.
Thanks for helping!
You are absolutely correct. Thanks for pointing out that mistake. I just corrected it.
Great information and presentation. I like both the written text and video. This will be a lesson revisited a few times until I understand it completely. Thanks for a fantastic course so far!!
Awesome! I am so glad that you are enjoying the course and learning. It’s a great idea to revisit pages until you fully understand them. Rather read something multiple times than rushing it.
Wow, So glad to read this. But I still have a question regarding volatility. Says up there that option buyers can benefit from rising volatility. You mean buy the call option when volatility is high and sell it before expiration when volatility came down, because that’s also when the stock price would rise?
And when selling a put, sell it when volatility is high, that’s also when underlying will be low and option prices high, then buy back when volatility goes down and therefore option prices lower and underlying will be higher ?
Thank you for the comment, Eve.
Options tend to be more expensive in times of high implied volatility and options tend to be cheap in times of low implied volatility. Therefore, it is best to buy options when IV is low (because the options should be cheap then). Selling options, on the other hand, is best done in times of high IV (as the options will be more expensive then and you can thus collect more money when selling).
Furthermore, short option positions (e.g. short calls/short puts…) usually, gain value from decreasing IV which is another reason to sell options in times of high IV.
Long option positions (e.g. long calls/long puts…) profit from increasing IV.
So to recap, options buying strategies are best suited for times of low IV, whereas options selling strategies are better suited for high IV environments.
For each single option strategies can you define the best time to buy and then close the option strategies using iv? For example when is the best time to buy calls then close the position focusing on iv, when is the best time to buy puts then close the position focusing on iv, the best time to sell puts, then close and sell calls then close in what iv environment? I had a different question that I included here last night but don’t see it here. Thanks in advance.
Louis, thank you for this lesson. Somehow, I was unable to see it earlier, therefore I sent another question that you can disregard. Really enjoy this particular segment because it has been of great value to my understanding and progress in option learning. Most video’s and reading material are very vague on the subject confusing many people out there, including me. Thank you again.
Glad to hear that you are learning from my content. If you ever have any other questions, I will be happy to answer them.
Louis, thank you for responding so very quickly to my email about having trouble posting comments after each lesson.
I posted the comments through my laptop. I am posting this through my iPhone. I hope this solves my problem with posting.
TRADEOPTIONSWITHME.COM IS THE BEST SITE TO LEARN OPTION TRAINING. YOUR TRAINING IS BETTER THAN ANY PAID FOR SITE.
HERE ARE JUST SOME OF THE REASONS:
WEBINARS
VIDEOS
FREE CHARTS
COMMUNICATION
THE LESSONS ARE WELL WRITTEN WITH LOTS OF EXAMPLES
THANK YOU FOR YOUR DEDICATED MENTORING.
JOEL CULPEPPER
Hi Joel,
Thanks so much for the kind words. I truly appreciate them! I am also glad to see that the problem with the comments is no resolved.
I started my journey on options about 5 month ago and I made a whole lot of research trying to understand how each element works…and I got stuck with the geeks. The more I search the less I understood and the more confusing it got therefore my paper trades always tipped the balance on the losing side.
Than I discovered your site and realized that my whole life was a lie…lol, my option life at least. I can finally get a good grasp of the famous Greeks. I mean I really understand the way you explain each one of them…now applying them accordingly is a story for another time.
Thank you Louis, you just turned on the light in that dark room for me. I mean big time. As I documented all my trades I will go back to them and try to make sense of it all by comparing the Greeks. In the moth or years to come when I am profitable, I will remember you as the one who shade the light and made it all come together.
From Haiti with respect,
sf
Thank you so much for this very kind comment. I really appreciate it! It is just awesome to see that my content could finally help you understand the Greeks. If there ever is anything else you get stuck on, make sure to let me know and I will do my best to help you out. Once again, thanks!
In your explanation of delta, with an underlying px of $200 and a delta of .40, do you not mean the premium would increase by $40 if the stock price moves to $201 (not $40) and would decrease by $40 if the stock price moves to $199 (not $39)?
Hi Rich,
Yes, you’re right. Thanks for pointing this out.
Very good and easy to understand. Thank you.
Living in the UK can you recommend a broker account as the better ones seem to be America only?
Hi Kevin,
I personally use tastyworks as a broker. They also accept UK customers. You can check out my tastyworks review here.
Many thanks Will do
Just to make sure I’m following, long = buy and short = sell?
Yes, that’s correct.
Very informative/educational, even though I have been reading other articles, these are the best yet!! Learned a lot that I thought I already knew, but didn’t really know!
Hi Bobby,
Thanks so much for the kind words. I really appreciate your comment and am very happy to hear that you like my content.
THere is IV for both PUT and Call side. Which one do we consider?
To calculate the IV of the underlying, typically a weighted average of the ATM options’ IV for both calls and puts is used.
Hi Louis
First of all I am so fascinated with your article. My question
Do you have any article where you explain Moving Average convergence & Divergence -MACD-
Thank you.
Hi Fouad,
Thanks for the comment. Sadly, I do not yet have such an article.
Hi Louis – Just to let you know that I have benefited tremendously from your learning materials, it is a pity that they have not received wider recognition in the internet /trading community. I suppose one of the reasons is that people always believe they can run before they master the basics of walking. I shall keep coming back to your course materials – have purchased your spreadsheet and trading guide.
HI Alwin,
Thank you so much for the positive feedback and continued support. I truly appreciate it!
Hi Luis,
Thanks again for sending this article. Its very educational and you explained very nicely. Your articles are certainly helping me to learn basics. I hope all this learning help me when I start trading. When I start trading you will be first one I send an email thanking you for all the teaching. I am slowing gaining confidence.
Thanks again for all your help
Hej Louis,
Thanks for the detailed explanation.
I am new to this environment and not very good at calculations, but I am trying my best to fully understand it.
I am a bit confused in the Gamma Example.
When you point out that ” If ABC’s price decreases by $1, Delta decreases by 2 as Gamma is 2. If ABC drops down to $198, the overall loss would be $78 ($40 + $38). ”
You meant if it drops to $199 instead ?
Cause if it drops to $198, then the price is decreasing in $2, therefore Delta would be $80 and Gamma 76? or 36?.
Thanks and thanks for helping .
Hi Gonzalo,
Thanks for the question. I can certainly see how this can be confusing.
I did, in fact, mean $198 and not $199. Let me try to explain why. When ABC’s price is at $200, Delta is 40. This means that for a $1 decrease in ABC’s price, the option loses $40. So if it moves down to $199, the loss would be $40. At $199, the new Delta now is 38, so if ABC now drops down to $198, the new loss would be $38 + $40 = $ 78 and the new Delta would be $36. Note that for this example, we assume that Gamma is constant which usually isn’t the case in reality. But you don’t ever have to calculate anything like this by hand.
In simple terms, Gamma just is the rate of change of Delta.
I hope this clarifies the confusion. Otherwise, definitely let me know.
Hi Louis, thank you for your course.
“Therefore, a bearish option position can still gain value even if the underlying asset increases in price if the position has a (very) negative Vega-value. In this case, the decrease in IV would offset the loss from the underlying asset’s move”.
I’m confused with this sentence.
Let’s say that you have a bearish option position (e.g. short call?).
I understand that if the underlying asset’s price increases, the options’ price increases (deeper ITM or closer to get ITM). From this perspective you lose money because you have shorted a call and you need to close your position eventually, you need to buy your call back for higher price.
On the other hand, your Vega is negative and increase in the S(stock) means decrease in IV, ok up to this point. But, how does the decrease of IV leads to decrease in P(option’s price)?
Thank you,
Labros
Hi Labros,
From your explanation, I can’t really tell what part you don’t understand. You explained it completely right. The position loses since it has a negative Delta and thus an increase in the underlying’s price is bad, however, if the Vega is more negative and IV drops enough, the position will profit from the drop in IV.
I am a senior close to 80. I have decided to study your course to stay mentally challenged and perhaps make some money with the knowledge. So far I really like the way you have presented the course – in clear and easily digestible portions in videos, text and diagrams.
While your definitions of ITM and OTM are technically correct, it is not always easily remembered in the heat of the moment. So I ask the question- Can I profit from the strike price? if the answer is yes, then it is ITM. if the answer is no, then it is OTM. This question forces me to think it through logically and in line with the option trade objective.
I am now in the intermediate course getting my head around the greeks. First go-around, it was truly all greek to me! (pardon the pun). But now it is slowly sinking in. Thanks for a great course, Art
Hi Louis,
Thank you very much for submitting Stock Options Pricing and Option Greeks Explained.
It will take me a few days to learn it – I have basic knowledge – think I’ll study it on the weekend and do a quiz, which I’ll tell you about inform.
I will contact you for any questions!
Best Regards!
Hi Lois,
Once again, thank you very much for your education. I am studying this fantastic material about Options and when I return the answers to the Quiz you will know that the dream has covered those Lessons.
Cheers!
Slobodan
Hi Louis
Thank you for explaining the greeks so well, I found the table is quite useful to stare at. Following on Eve’s line of thought on volatility, you can purchase an option (such as vertical spread or condor) with a lower price at low volatility and sell at higher volatility. But for defined risk and defined profit option strategies, they all involve a long and short combinations of call or/and put, so the Vega values tends to cancel out. Is there an option strategy that has an inherently imbalance Vega values so that it has net positive? If so, wouldn’t it be possible to setup a trade with consistent gain?