This article is part of an options trading course. Previously in the course, you (could have) learned what options are and how they work. In the last lesson, I presented option basics like strike prices, expiration dates, different option types, going long or short etc. These things should not be new to anyone reading this article. If you are new to these terms, I strongly advise to check out the previous lesson: Options Trading Basics.
In this lesson, I will introduce you to Implied Volatility (IV) and Implied Volatility Rank (IV Rank), two very important concepts when it comes to options trading. Furthermore, you will learn about option trading strategies. But keep in mind that this simply is an introduction, you won’t learn specific option trading strategies in this article. The concepts learned in this lesson are necessary for future lessons (in which you learn specific option trading strategies). So make sure to go through this lesson before continuing to anything more advanced.
Stock Option Trading Strategies
As you may know, options can vary in many different aspects. There are different types (call options/put options), expiration dates and strike prices to choose from. This means that there usually are a lot of options available to trade for one asset. Just to give you an idea, SPY (a very popular and well-known ETF) has well over 1500 options available to trade (at the time of writing this article). That is a lot of options! Just compare this to stock trading. Stock trading gives you two possibilities, either you buy shares or you sell shares. Options trading literally gives you thousands, if not even more possibilities to make money. There is an options strategy for every market scenario imaginable.
Besides buying or selling individual options, you can also combine different options to create multi-leg option strategies. This opens a whole new realm of possibilities. Not only can you buy or sell 1500+ different options on SPY, you can also combine as many of these different options as desired. Therefore, the possibilities are literally endless.
This might seem somewhat overwhelming, especially for beginners. But don’t worry, even though there are unlimited possibilities, you only really need to know a handful of option strategies. Some of these simply consist of two different options. But more on specific stock option trading strategies in a later lesson.
Defined vs Undefined Risk Strategies
There are two different types of option trading strategies:
- Defined Risk Strategies: Just like the name implies, defined risk strategies have a defined risk. This means that these strategies have limited risk meaning that you can’t lose more than a certain amount. Most long strategies are defined risk strategies. Defined risk does not necessarily come with defined profit potential. Some long strategies (e.g. long calls/puts) have an unlimited profit potential. But this may vary from strategy to strategy.
- Undefined Risk Strategies: Opposed to defined risk strategies, undefined risk strategies don’t have limited risk. Therefore, you don’t know how much you can lose when trading undefined risk strategies. As far as I know, undefined risk strategies always have defined profit potential meaning that your upside is capped when trading these strategies. A short call/put is an undefined risk strategy.
Even though defined risk strategies may seem like an obvious choice, they aren’t. Besides risk and profit potential there are other aspects to consider as well. For example, the probability of profit (POP) is an extremely important aspect when it comes to options trading. Many undefined risk strategies have a higher probability of profit than most defined risk strategies. Therefore, undefined risk strategies may be preferable.
Payoff Diagrams Explained
Understanding how different option trading strategies behave for price changes in the underlying asset can be quite hard. That’s why payoff diagrams were created. Payoff diagrams also known as payoff profiles visually display changes in the option strategy’s profitability for changes in the underlying’s price. In other words, they show how the profit or loss of a strategy looks like (at expiration) for price changes in the underlying asset.
The easiest way to explain this is with an actual payoff diagram. The Y-axis of a payoff diagram stands for the profit and loss in the position and the X-axis displays the price of the underlying asset.
The payoff diagram below is that of a 1 share long stock position (entry at $100). Most people know how a long stock position works. For every $1 move up in the stock price, the position gains $1 and for every $1 move down, the position loses $1 of its value (without commissions factored in). That’s why the graph is increasing linearly. As you can see, the (Profit/Loss)-axis is at zero if the stock price is at $100. But if the stock price increases to $105, the (Profit/Loss)-axis is at $5 meaning that an increase of $5 in the stock price will lead to a profit of $5 in a 1 share position.
The payoff diagram of a long stock position is still quite simple. But it is a good and simple way to understand how payoff diagrams function. I will now present a few more payoff diagrams of relative simple option strategies.
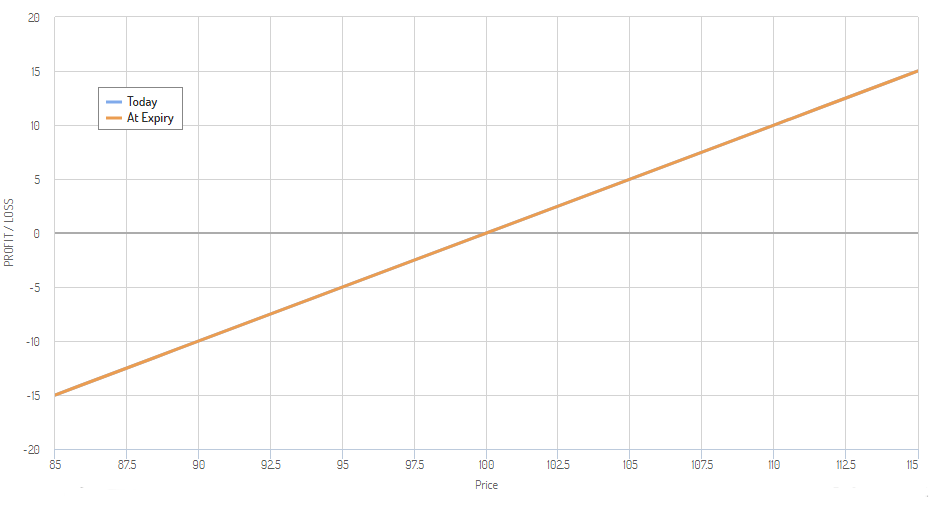
Here is a payoff diagram of a long call on the expiration date. As you can see, a long call is a defined risk strategy. If the price of the underlying moves below the $100-mark, the max loss will be achieved. The loss in a long call won’t increase for further price falls in the underlying asset. However, the reward is unlimited for long calls. The further the stock price increases, the greater the profit in the long call becomes.
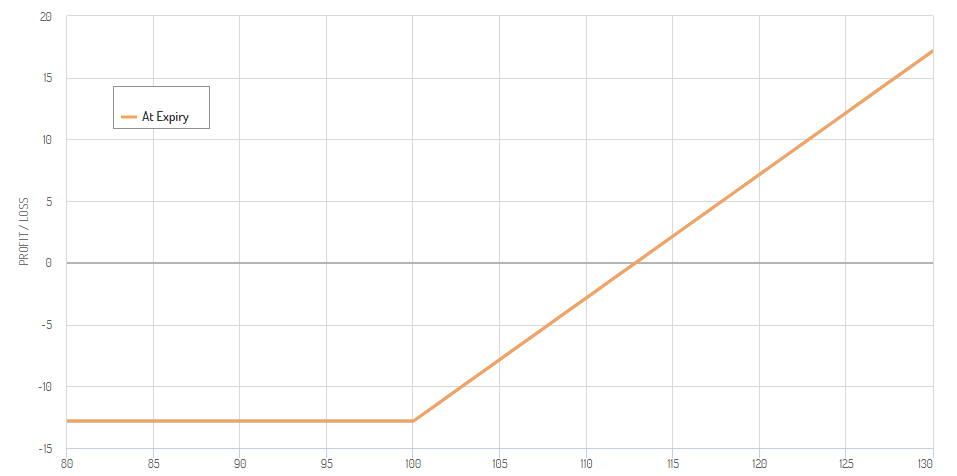
The following payoff diagram is that of a long put at expiration. It looks very similar to that of a long call, the only difference being its direction. Long puts are defined risk and undefined profit strategies as well. They profit from decreases in the underlying asset’s price.
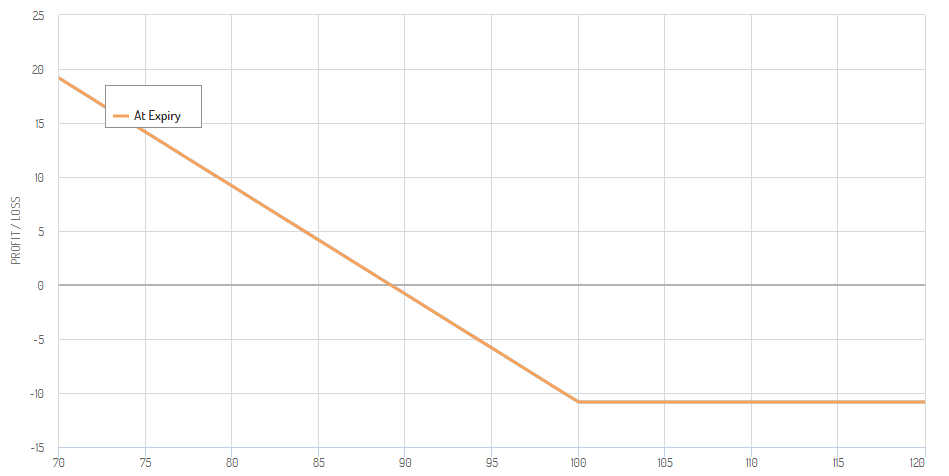
Now, I want to present a payoff diagram of a short call at expiration. It looks just like the payoff diagram of a long call turned upside down. Short calls have limited profit potential but unlimited risk. The further the underlying’s price increases, the greater the loss in the short call position becomes. But no matter how far the stock price decreases, the profit in the position won’t increase after a certain point.
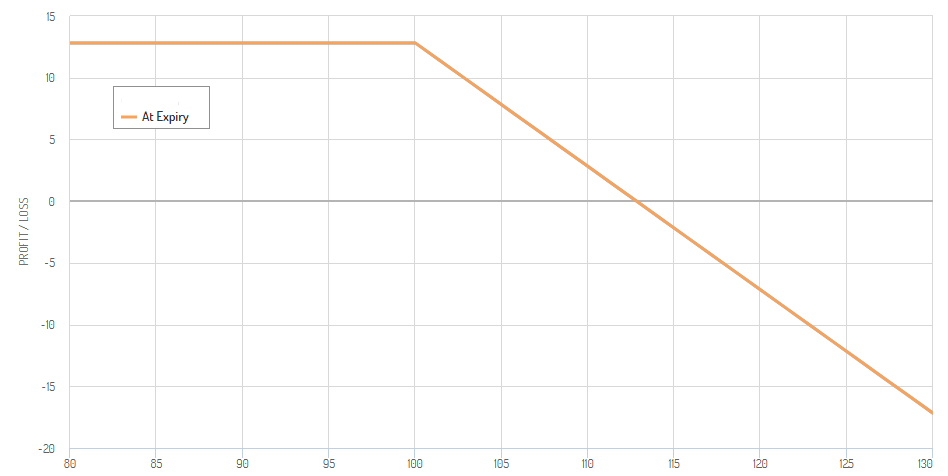
Furthermore, here is a payoff diagram of a short put at expiration. It works like a short call just the other way around. The short put profits from an increase in the underlying asset and the position loses value from a decline in the underlying’s price.
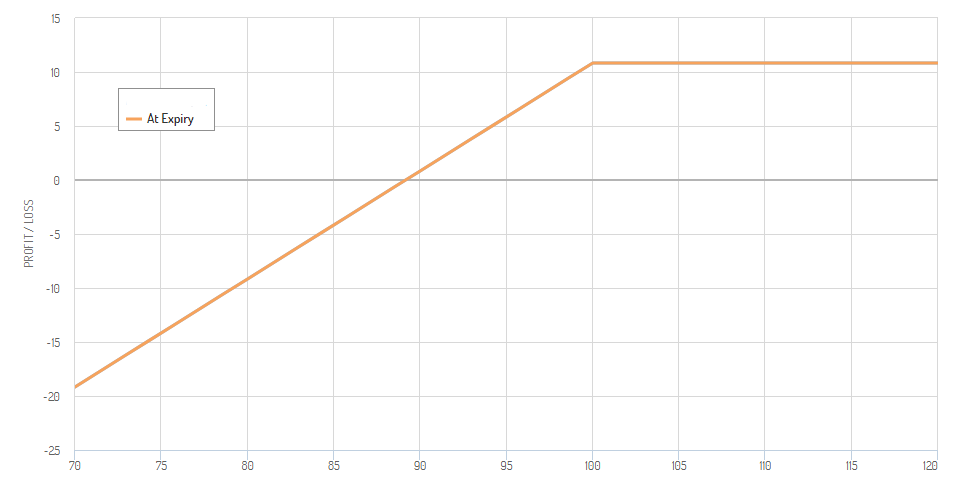
Last but not least, I want to show a payoff diagram of a more advanced option strategy to give you an idea of the possibilities that options give you. The following strategy is a call broken wing butterfly. It is both a defined risk and a defined reward strategy. I won’t explain more about this strategy in this lesson as it isn’t important for now. Nevertheless, I hope the payoff diagram can give you a good impression of option’s versatility.
Implied Volatility Explained
Check out the following video lesson in which I break down what implied volatility is, how to use implied volatility and why it is important:
Implied Volatility (IV) is a very important concept when it comes to options trading. Every options trader should know about implied volatility. Furthermore, implied volatility is a major component in options pricing. In this article, I will explain some of the most important IV basics but I won’t go too deep into this topic. But don’t worry, you will hear a lot more about IV in later lessons.
Implied volatility can be thought of as the expected volatility of an underlying asset during the life of an option. With the life of an option, I mean the time until an option expires. Note that together with option’s pricing, expectations and supply and demand implied volatility can change. In other words, implied volatility is not a constant.
As implied volatility can change, it can increase or decrease. In times of high IV, options tend to be more expensive and in times of low IV, they tend to be cheaper. Therefore, many option traders like to sell options when IV is high so that they can potentially profit from a decline in IV. Option buying is more popular in times of low IV, as this gives buyers the possibility to profit from increases in IV.
It is important to understand that implied volatility is derived from option’s prices and not the other way around. When people expect bigger price swings (aka. more volatility), the demand for options increases. Thus, the option’s prices increase. With formulas like the Black Scholes model, one can then find out what the implied volatility is.
Don’t think option’s prices are high because of the high implied volatility. It is the other way around, implied volatility is high because of high option’s prices.
How to know if Implied Volatility is High or Low – What is IV Rank
Finding implied volatility for different assets usually isn’t hard. The hard part is to find out if IV currently is high or low. Normally, you won’t have any references to past implied volatility stats and comparing to the IV levels of other assets doesn’t make sense either as IV is different for every asset. Therefore, you can’t really recognize if IV currently is above, below or around average.
To solve this problem, Implied Volatility Rank (IV Rank) was created. IV Rank compares the current IV level to historical IV figures on the same asset. IV Rank is a number between 0 and 100. 0 is the lowest possible IV Rank and 100 the highest. An IV Rank of over 50 means that IV currently is relatively high and an IV Rank of under 50 means that IV is relatively low. The closer IV Rank gets to 0 or 100, the lower/higher implied volatility is.
Usually, IV increases in times of falling prices whereas IV often decreases when prices increase.
Continue to the Option Beginner Quiz: HERE

Hi, Louis.
I have a little experience trading options. I think a lot of people shy away from options because they don’t really understand them.
Basically, and option is the option, but not the obligation to buy (call) or sell (put) a particular stock (underlying) at a particular price (strike price) up to a certain date (expiration).
You graphs certainly do a good job of explaining how these things work. You can easily see from your graphs how you make money from call options as the price of the underlying stock rises, and you make money from put options as the price of the underlying stock decreases.
Do you think option trading is for everyone ,or are there some people who should stay away from it?
Greatings Andy,
So to your question if options trading is for everyone. In my opinion nearly everyone can learn how to trade options and profit from this. But the key point here is the learning part. Without the correct education it is extremely hard to earn money in the stock market. So I think options trading is for everyone who is willing to put in some time for education first.
Hello,
I have been interested in options trading for quite a while. I have studied a lot on this subject and I found out that a profitable but risky strategy can be short selling. Of course, if you know what to do, this strategy can give a nice return and make you money. What do you think about that? Would you recommend it? I’m looking forward to read your next article on this topic.
Keep up the good work
Hey Francesco,
You are absolutely right!!! This will be the options trading style which I will cover the most on this website. Short premium selling is one of the best options strategies out there. And actually it isn’t so risky at all (if you do it correctly which I will teach you). I will write some articles/pages about this short premium/high probability trading in the near future.
A lot of information and excellent post to learn from this strategies but I’m a bit confused with the 16 graphs throughout this post.I’m not an expert, but it is something that I would like to learn.
thanks
Hey Jairo,
The graphs are payoff diagrams of different option strategies. Like I said in the end this was just to leave an impression on you have a rough idea of what option strategies. But if you are interested in learning more about specific option strategies you should definitely check out the Strategy Section here.
Education is key in profitt trading. Knowing what to do and what not is very important in this especially with the defined and undefined risk strategy which I think will be helpful when diving into, because of the turn around that could surface at the aftermath. Knowing those is unique and also an eye opener.
Happy to help.
Louis, I’m a little confused with your 2sentences about iv. You said above “Don’t think option’s prices are high because of the high implied volatility. It is the other way around, implied volatility is high because of high option’s prices.” Then farther down you said “Usually, IV increases in times of falling prices whereas IV often decreases when prices increase.”. Isn’t that a contradiction?
Thanks for the comment Eve,
That is a great question. During the second statement, I am not talking about the option’s prices. I am talking about the prices of the underlying asset.
For instance, if a stock’s price is falling a lot, the IV of its options will likely rise. If that stock now reversed and began to rise again, then IV would likely go down.
That’s also why IV tends to be very high during market crashes/bear markets.
The first statement simply says that implied volatility is derived from option’s prices and not the other way around.
I hope this makes sense. Please let me know if you have any other questions or comments.
Nice and detailed Article here. Studying rate is getting much slower now since thorough comprehension is becoming more tasking. Thanks to this detailed article though, I was able to understand. ?
I got 10/10 ? in the quizz but seriously, I got confused in the IV region.
Although after reading your reply above to Eve, things became much clearer. But I will love to understand a statement you made.
The statement goes like this – “…many option traders like to sell options when IV is high so that they can potentially profit from a decline in IV”.
Talking about “sell”, I assumed you’re referring to short calls or put. Now, two things are happening at once in the statement. “High IV” and “decline in IV” so I got confused.
My question is this – Even though the IV is high, will the selling of options by sellers make it start declining? OR do you mean a reduction in the underlying asset’s price (which is favourable for short call options and also is the reason for increase in IV) makes options sellers want to sell in order to make profit (since the condition is favourable for short calls).
I’m sorry if I seem to confuse you. It’s because I don’t really understand the statement.
Thanks a lot for the detailed article. Hoping to push through all the resources here even though I feel so overwhelmed knowing I still have a long way to go. ?.
Thanks once again for the hard work done on this blog.
Thanks for the question. It is totally normal to have difficulties understanding everything right away. So don’t worry about asking questions. I am more than happy to help.
Just like a stock’s price, implied volatility also changes over time. With options, you can’t only bet on moves in the underlying asset’s price, but also on moves in its implied volatility. For instance, short options profit when implied volatility goes down, whereas long options profit from increases in implied volatility.
This might still be quite hard to comprehend. That’s why implied volatility is covered much more throughout the intermediate and advanced course. I recommend checking out my article on options Greeks and options pricing. It is the first article of the intermediate course and in it, this topic is covered in more detail.
Make sure to let me know if you have any questions or comments after reading it.
Ok! “you can’t only bet on moves in the underlying asset’s price, but also on moves in its implied volatility”. I think this one cleared it for me.
My initial thought was that as you bet on the moves in the underlying price assets, you’re automatically betting on its Implied Volatility. I think it’s getting clearer to me now. Obviously there is still much I need to know.
I know I’ll figure it out properly down the road as I read more on it.
I’ll check out the article now.
Thanks for your kind reply. Really, Thanks!
You are very welcome.
Hi Louis,
As I understand it, and as you’ve explained, IV is defined as an annualized 1 standard deviation range for an underlying. So what is the meaning of implied volatility for a strike?
The IV on each strike is calculated by inputting the market price of the option into the Black-Scholes model. If the pricing model calculates IV per strike, how do you get a value for the underlying as a whole? For example Tastyworks says that for January expiration SPY has an IV of 21.7%. Is this an average or other aggregation type formula that combines IV from all the strikes? Is there such a standard formula or do other trading platforms it differently?
For example the 250 put on SPY is 20 points out of the money and has a 23.76% IV. Does this mean that someone buying the 250 put for the current market price is valuing the volatility for this cycle at 23.76% and say someone else buying the at the money put (270 with 18.7% IV) for the current market price is measuring the volatility for this cycle at a lesser value?
What I am trying to get at is:
– How do we find the IV for the stock (as i assume this is the IV that was being mentioned in your post)?
– Is the IV for the stock just an average/aggregate of all the IV strikes for all option contracts?
– When determining IV to use in our strategies, do we care about individual strike IV’s (since they are all different), or just the IV of the entire stock? i.e. if the IV on the Stock is 80% and has a IV rank of 70, but the IV % on the strike price im considering to trade is 95%, which do we use?
– lastly, there are IV percentages that are over 100%, what does that mean?
Thanks, sorry for the long question.
Hi Tim,
Thanks for your comment. First of all, I want to clarify that IV is a purely theoretical value that tries to assign a number to the volatility premium of options. As you have noticed correctly different strikes have different IV values. This is somewhat counterintuitive and is often considered a flaw of the Black Scholes model. Check out my article on the Black Scholes Model for more on this.
The IV value displayed in tastyworks (and other broker platforms) is usually a weighted average of the IV values of ATM options.
I’d recommend putting most emphasis on IV Rank (and the IV value displayed), but you certainly can compare the IV values of different strikes to get an idea how the theoretical volatility premium is distributed. IV Rank tells you much more since it takes past volatility values into account.
Lastly, an IV of 100% implies that a one standard deviation move for one year is 100% of the underlying’s price. Here is an example:
XYZ is trading at $200 and has an IV of 100%. This means that a one standard deviation move for the next year is $200. Broken down to a day, this would be plus/minus 100/sqrt(256) = 6.25% or $12.5 (256 instead of 365 because the market has about 256 trading days). This, however, is just a rough estimate for the expected one standard deviation move calculated from the given IV. The actual price behavior of a stock on a given day can vary widely from this. Usually, stocks don’t have this high IV values for any extended periods of time.
I hope this helps. Make sure to let me know if you have any other questions or comments.
Hi Louis,
Thanks for the super fast, and thorough response. I looked at your Black Scholes article, and I skipped the math portion and read through the IV smile, and the setbacks of the BS model. I understand now that not all the strikes are used when calculating the IV for the stock, but which option contract then is being used when calculating IV for the stock?
There still has to be a specific option contract that is being used when calculating the IV for the stock, and using all the inputs from that option contract, correct? I read from other sources that it is the ATM/near ATM contracts, as they are heavily traded, but those articles don’t specify which contract expiration cycle those ATM/near ATM contracts are associated with.
Thanks!
Hi Tim,
The specific method and model used to calculate the IV values displayed in tastyworks is too long to be explained in a single comment. But if you are interested, I highly recommend checking out this PDF in which it is broken down.
Other brokers often just use some kind of (weighted) average of multiple ATM options. I don’t know what their specific formula is. But such an average typically looks at a handful of the most ATM options of multiple expiration cycles (e.g. 10 and 38 days out) and then takes some kind of weighted average of these options. But like I said, the specifics can vary from broker to broker.
I hope this answers your question. Otherwise, definitely let me know.
Thanks Louis, this was very helpful! You have a great site and I’ve been learning so much. Keep up the good work. Cheers.
You are very welcome.
Hi Louis,
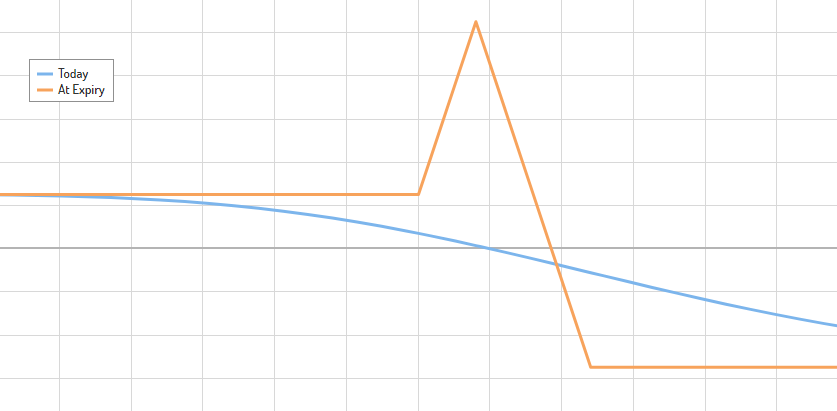
I have a question on the payoff diagram, specifically, the ‘today’ graph vs. ‘at-expiration’ graph. When we sell to open a short option position, we collect a premium, say $100. But according to the ‘today’ graph, we usually start off either at a loss, or substantially less than the credit received. Why is that? we already received the credit, so why do we have to wait until expiration to see the full profit?
thanks.
Hi Tim,
Thanks for the comment. Right after you open a position, you are neither at a profit nor at a loss (excluding commissions). Just like when you buy a stock for $100, you aren’t at a $100 loss right after the entry.
Even though you receive a credit to open a short option positions, you also have an obligation, namely to deliver/accept shares of the underlying asset for the strike price if the buyer chooses to exercise their right. To lose this obligation, you need to close the short option position. If you just sold the option for $100, you would likely have to pay $100 to close it again which means that you just break-even.
The idea is to slowly let the option lose its value and then later buy it back for less than you sold it for. You don’t always have to wait until expiration, but typically you will have to wait for more than a couple of days.
I hope this answers your question. Otherwise, definitely let me know.
Hi Louis,
I thought I understood the concept of IV rank and the number being between 0 and 100. Now I find that the IV rank can be larger than 100% if I look into stocks in the Tastyworks platform (which I understand you also use).
For example Xilinx today has an IV rank of 137.2
Why is that?
Thanks, Marc